INTRODUCTION:

An ellipse is an oval on a graph.

The equation for it is:

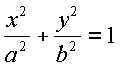  or    

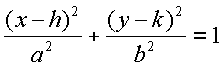
Like a circle an ellipse has a center. 

On the graph above the center is (0,0)

the distance from it on the both sides of the x-axis is equal. 

Same as the distances on the y-axis.

H and K tell you where the center is.

 If they it is not stated then the center is assumed to be (0,0). 

Is where X- point is H and the Y-point is the K.  

A and B equal the distant from the center. 

If it is the just a plain number on the bottom then take the square root

and that is your answer.

The axis with the most space from the center is the major axis,

and the least amount of space is the minor axis.

Foci are points within the ellipse.

Their coordinates (-c,0), (c,0) or (0,-c), (0,c).

They really depend on which whether the major is on the x or y axis.

a > b   the equation to find the foci c² = a² –  b² and

the major axis is 2a and

minor 2b. (-c,0), (c,0)

b > a > 0  the equation to find the foci c² = b²– a ²  

and the major axis is 2b and minor 2a. or (0,-c), (0,c).